Classification Part 2

Fundamentals of Machine Learning for NHS using R

Today’s Plan

 

• Classification
  • Decision Trees
  • Random Forests

Decision Trees

Decision Trees

 

• If you’ve every played “Guess Who?”, you’ve already experienced Decision Trees.
• The aim of the game is to identify the other players character by asking a series of questions, each question asked narrows down the possibilities, until finally we can identify the guess.

Guess Who?

• Out of the below what yes/no question would you ask first?
• Is your character male?
• Is your character wearing glasses?
• Do they have a moustache?
• Does your character have blonde hair?

Guess Who?

Asking if the character is male is the best first question, as it eliminates the most options, there are multiple hair colours, and not all the characters have hair!

However there is only the option of male or female in this case, and each character can be assigned to one or the other.

Guess Who?

 

• We could say that asking the characters sex results in the most Information Gain.
• The results of the first question, influence the next questions being asked. If female, questions like:
  • Does you character have a beard?
  • Is your character bald?
• No longer give any information.
• The Information Gain from these questions is zero.

Guess Who?

• Suppose I asked the following questions with these results to obtain this value.
• Is the character male? No
• Is the character wearing glasses? Yes
• Does your character have brown hair? Yes
• Is your Character wearing a necklace? No

Guess who?

 

Here is the entire decision tree for Guess Who?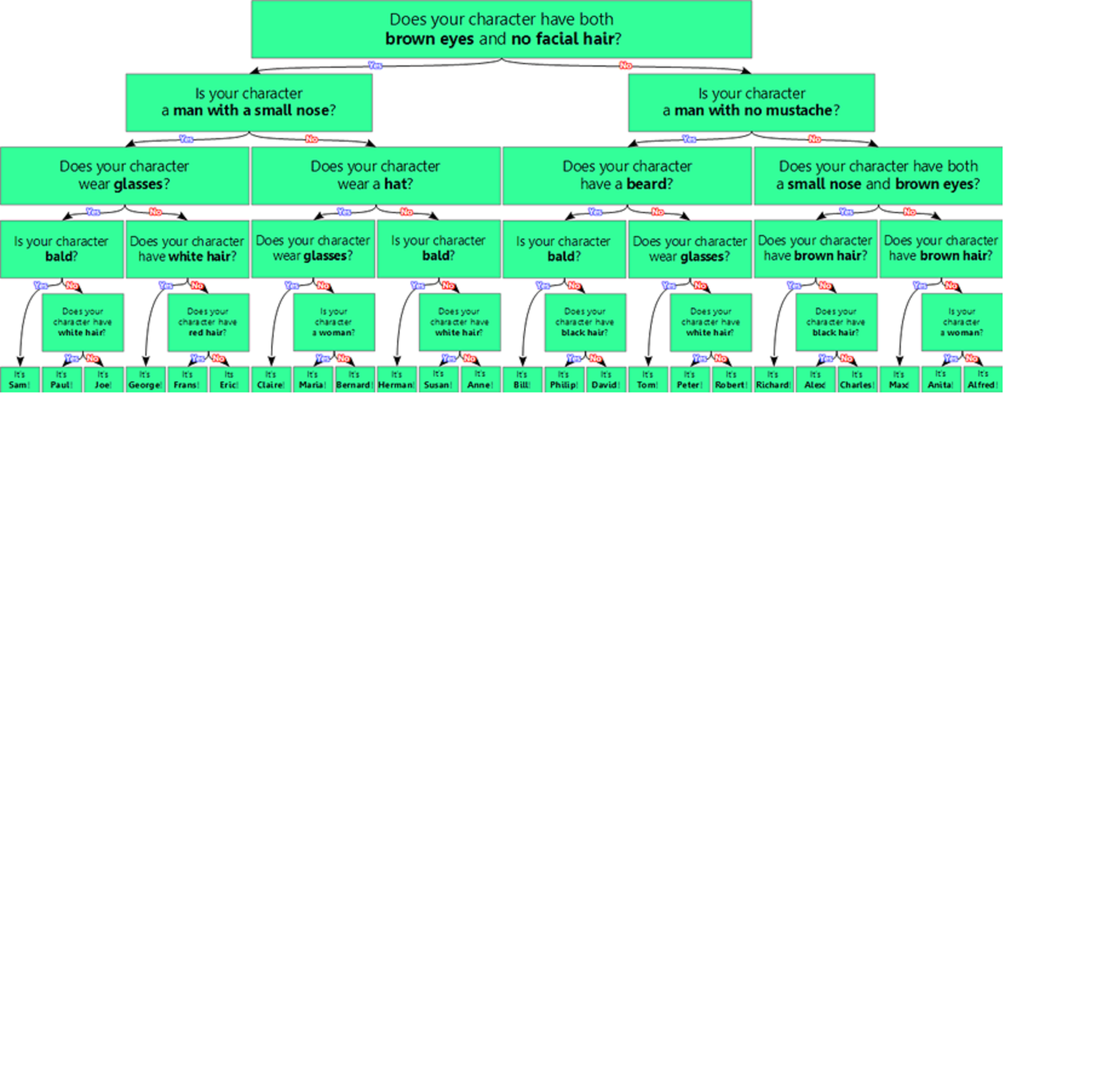

Information Gain - Simple Example

 

• Group 1 - are people who are sad.
• Group 2 - are people who are happy.
• We would like to predict whether or not a person is happy or sad.
• Based on how many days they work, and how many hobbies they have.

Information Gain - Example

 

The plot shows the number of days spent doing a hobby, how many days they work, and if they are happy or sad. What yes or no questions would you ask to determine if someone is happy or sad?

Information Gain - Example

 

Question 1: Do you spend less than 3 Days doing a hobby?

 

 

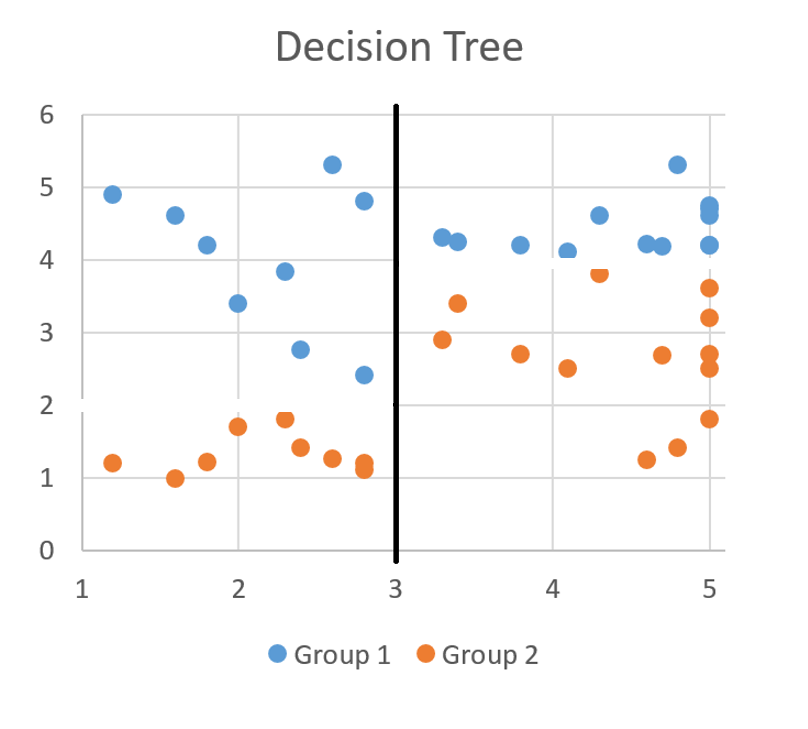
Information Gain - Example

 

• Question 2 : What would you ask if I said yes?
• Question 3: What would you ask if I said no?

Information Gain - Example

 

• What would you ask if I said yes?
• Question 2 : Is the number of days spent in work less than 2?

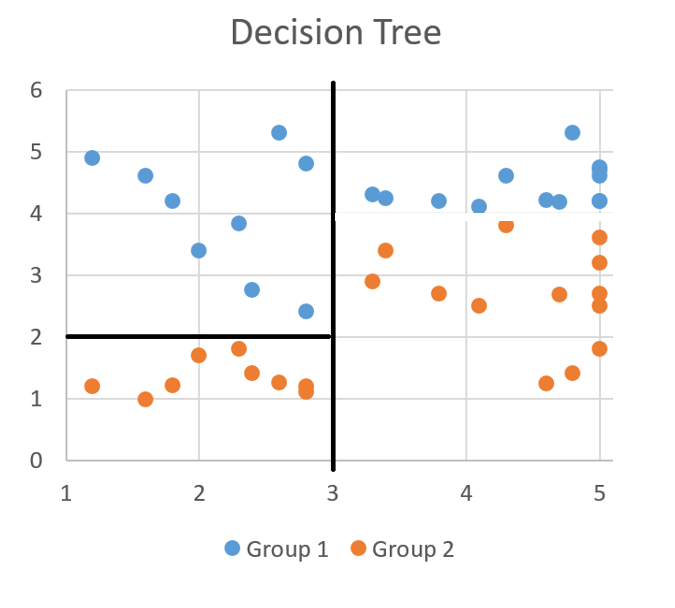
Information Gain - Example

 

• What would you ask if I said no?
• Question 3 : Is the number of days spent in work less than 4?

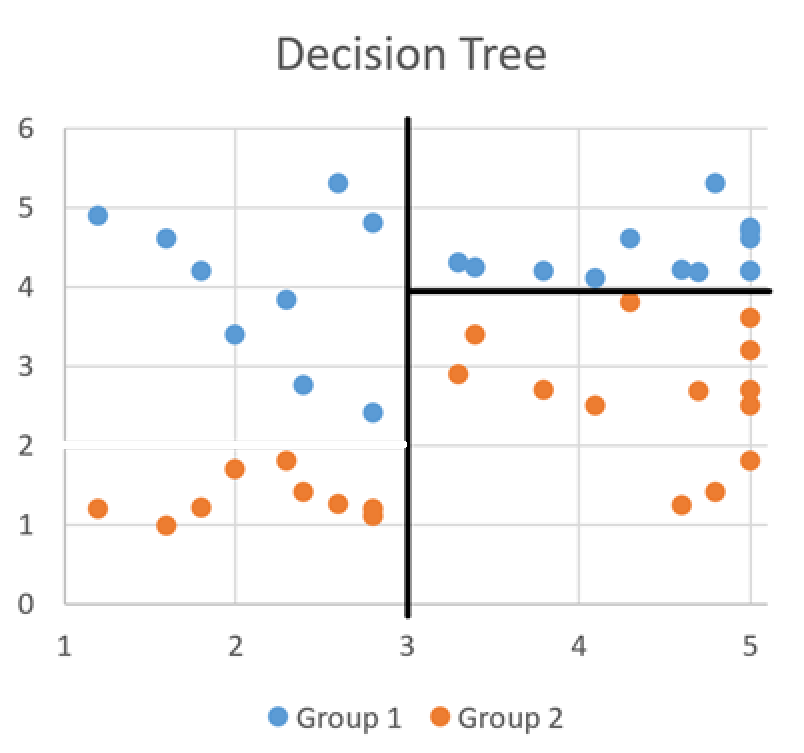
Information Gain - Example

 

Do you think we could use the model to classify if they are happy or sad? Y - is the number of days spent in work. X - is the number days spent doing a hobby.

 

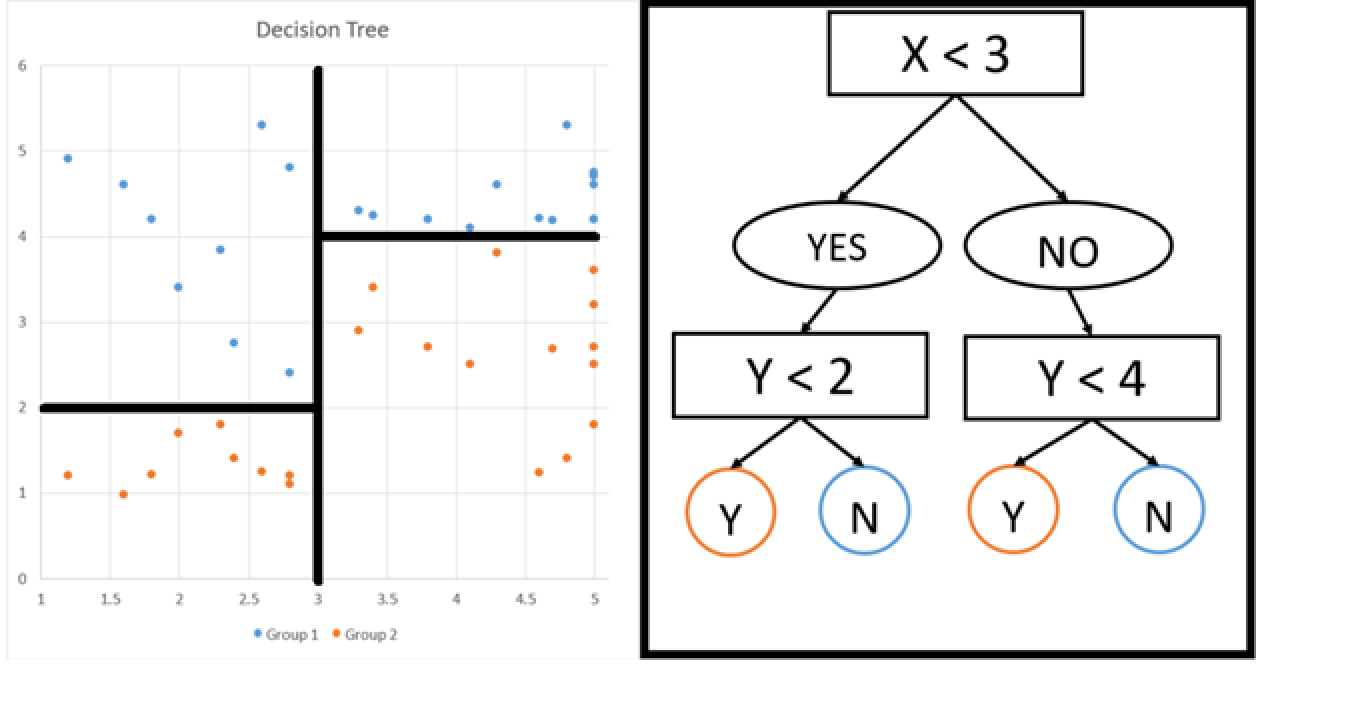
Information Gain - Example

 

For some additional data, collected in the same way, can our model predict if these people were happy or sad.

 

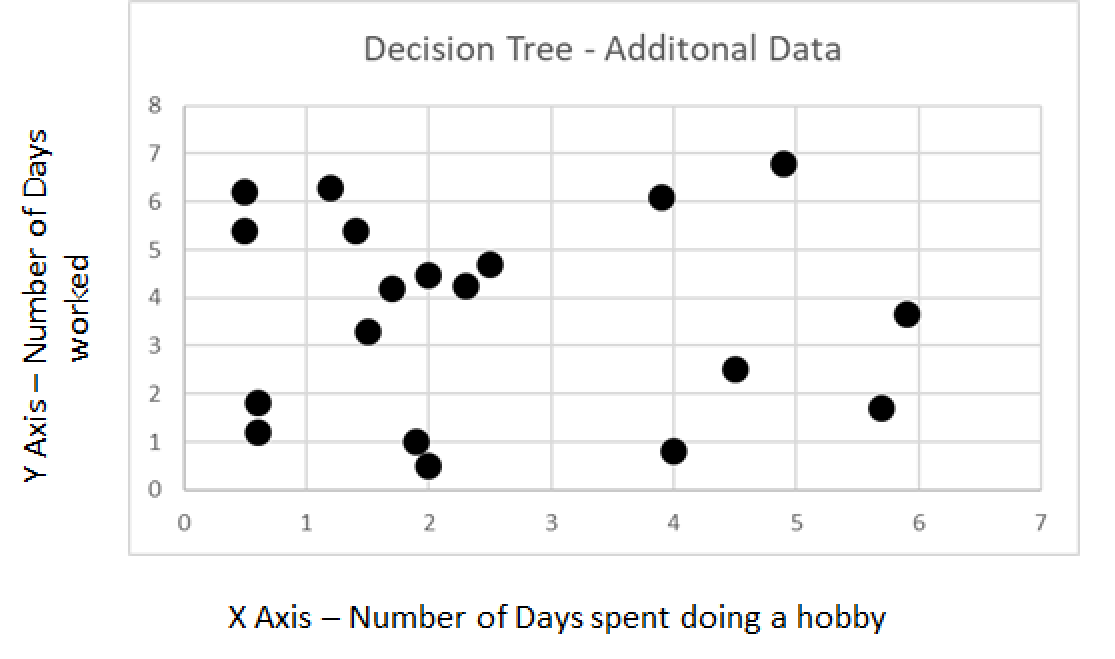
Information Gain - Example

 

Our model would suggest that these people were either happy or sad in the following way.

 

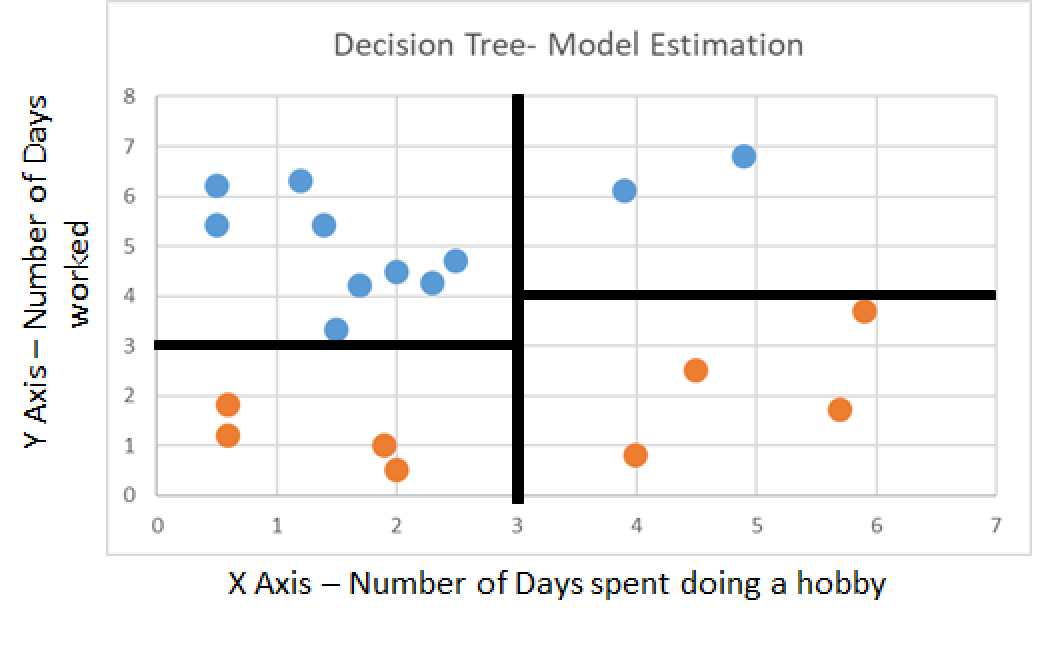
Information Gain - Example

 

Estimate groupings based on model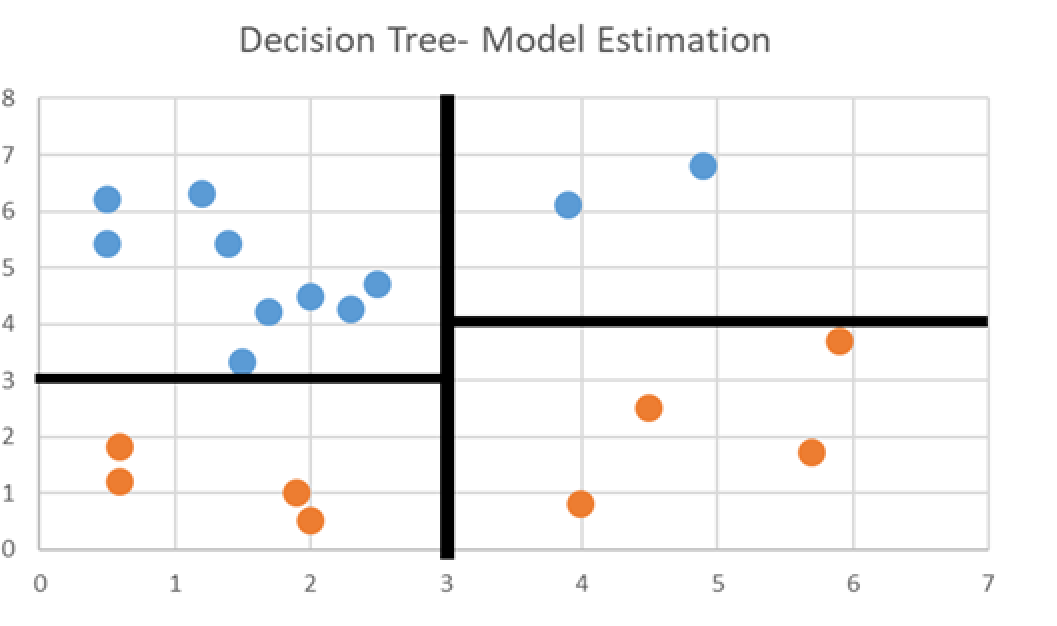

 

Actual groupings from collected data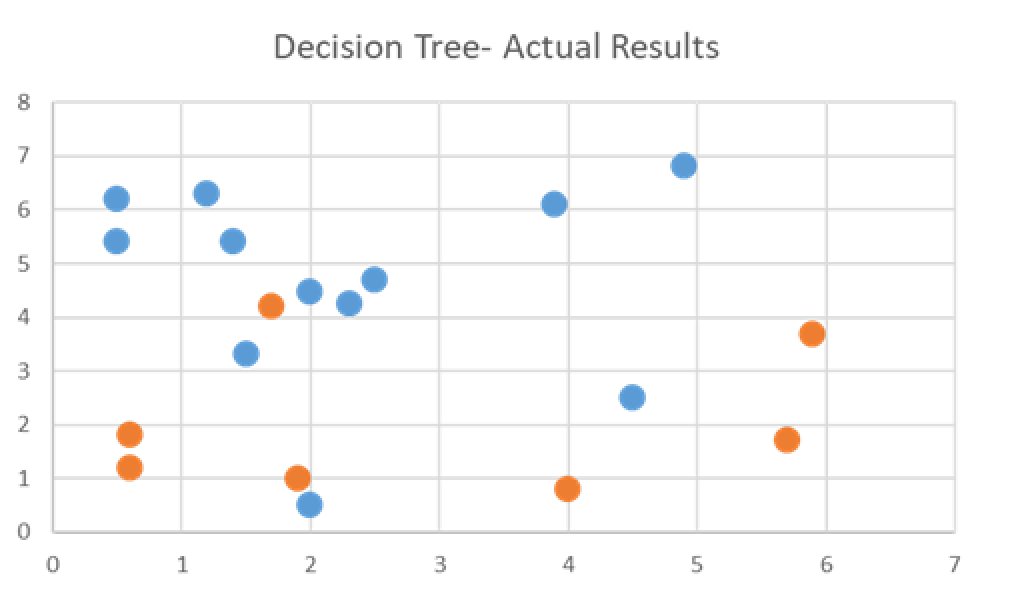

Additional data

 

• Overall the model correctly classifies most data points, attaching the appropriate “happy” or “sad” grouping based on the number of days spent working, and number of days doing hobbies.
• It does however misclassify some cases. These could just be anomalies, or if more features were collected, then perhaps the model would be more accurate.
• Remember Accuracy isn’t everything (also consider sensitivity and specificity).

Entropy

 

• Initially when discussing Decision Trees, using the GuessWho? example, we mentioned Information Gain.
• Notice that some questions, depending on the answer prior, no longer become relevant.
• Information Gain is derived from another factor, Entropy.
• Entropy links to Decision Trees, in that Entropy is a measure of on average, how many questions we would need to ask to know a result multiplied by the probability of each specific result occurring.
  

Entropy

 

In our example, “Do you have a beard”, is no longer a question that gives any information, that being it brings us no closer to our answer.

 

Entropy

• Entropy in a sense measures the randomness of an event.
• If I picked a character, and you randomly guessed who I was. This would have an entropy of 1 (complete random).
• If you wanted to guess my character, but knew he had short blonde hair and was wearing a suit. The Entropy would be 0, as you would be absolutely certain of the outcome (Alex).

 

Example

 

• I’m thinking of a number between 1 and 100.
• In the most efficient way possible can you guess it?
• Only asking questions of the form:
  • Is your number greater/less than x?

Entropy

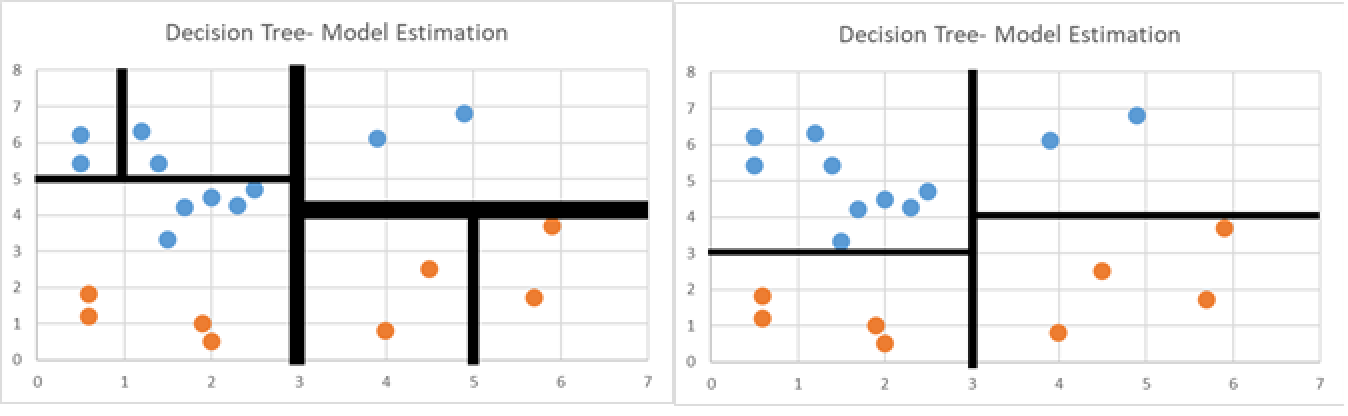
• Decision Trees that aim to have lower Entropy, have to ask less questions to solve the problem.
• While both below have the same accuracy, one has a much higher Entropy, and delves on overfitting.

Entropy v’s Information Gain

 

• Information Gain is an additional calculation on Entropy, that determines the usefulness of a feature.
• For example in our GuessWho? example:
  • Knowing that the character does not have a beard gives no information, as no character has a beard. Information Gain in this case would equal zero.
  • Conversely, if the resulting information, results in absolute certainty of the outcome of character, Information gain would be maximal.

Bagging & Boosting

 

• Bagging and Boosting successfully improve on standard Decision Tree’s, and fall into the category of Tree Ensemble Methods. Which lead on to Random Forests.
• Bagging firsts splits the data into a Training and Test set.
• From there, T sets of the data are made, where each set contains randomly selected samples with replacement.

Bagging & Boosting

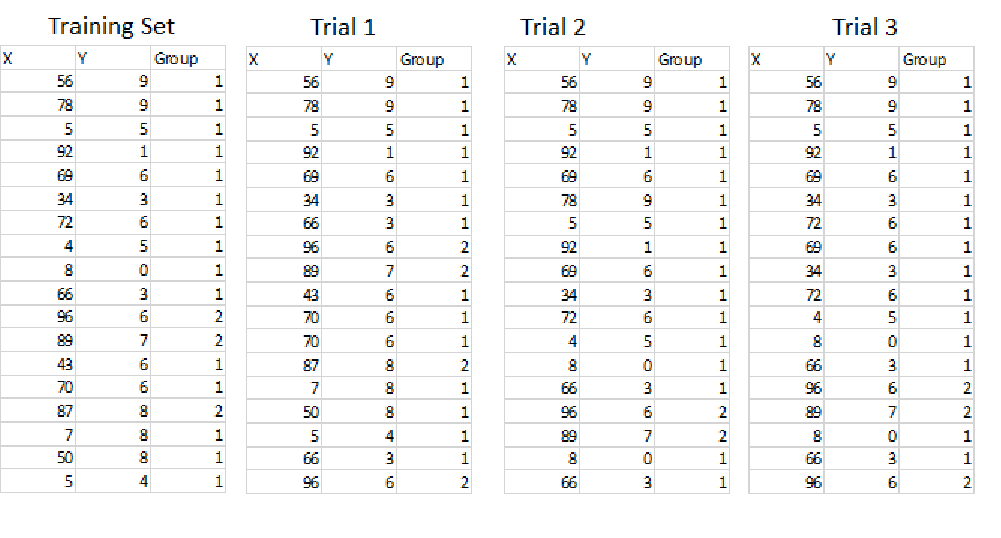
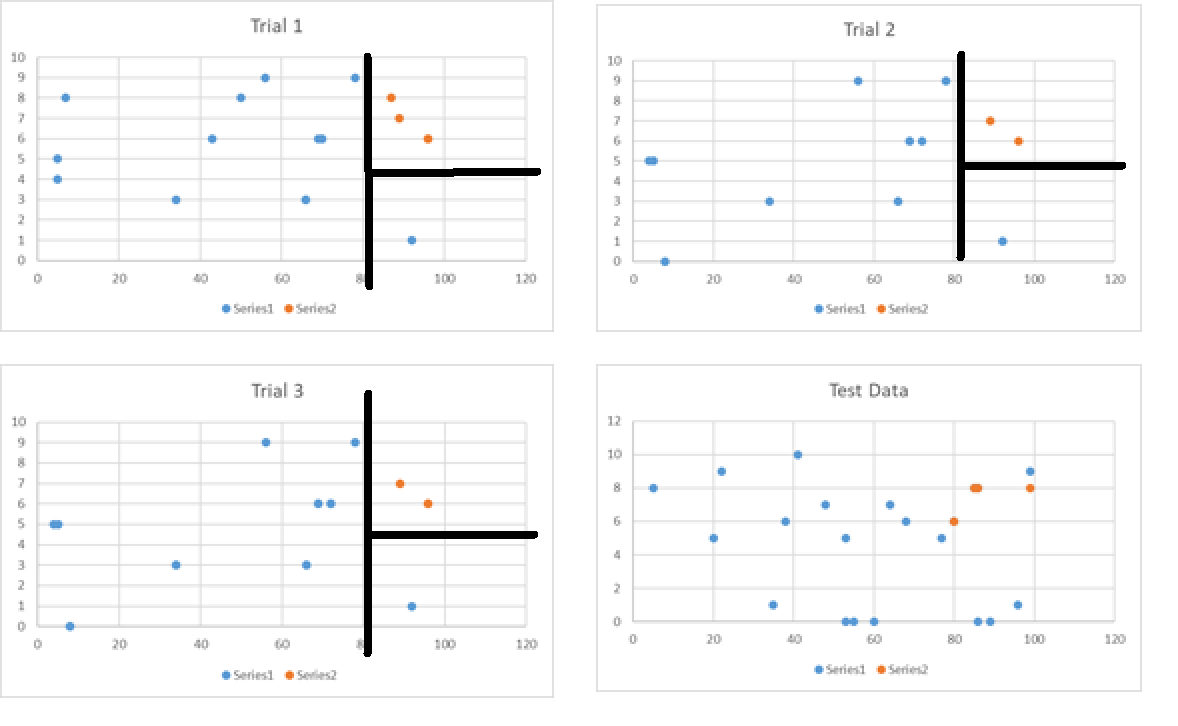
• Suppose I have a training set. With T = 3, so three trials.
• Notice that some examples are repeated.

Bagging & Boosting

 

• Due to the small sample size, this is an extremely inefficient method for Decision Tree Learning.
• In practice this stops the Decision tree model from overfitting, but here there is not enough information (data points).
• Each trial votes where they believe a certain data point belongs. The majority vote winning.

Bagging & Boosting

Bagging & Boosting

 

Boosting samples data in the exact same way as Bagging, accept instead of having equal votes: \[ Votepower = Vote*f(accuracy) \] This just essentially means that Decision tree’s with a higher overall accuracy, have a higher overall vote score.

Random Forest

 

• Within GuessWho? there are a number of questions.
• For your first guess, a Random Forest would subset these questions randomly so that you can only ask a few, say:
  • Is your character bald?
  • Is your character wearing glasses?
  • Do they have a moustache?
• You would then ask the best question out of these three.

Random Forest

 

• For the second iteration, the random sample may be:
  • Is your character wearing bunny ears?
  • Do they have black hair?
  • Are they male?
• And again you would ask the best question.

Random Forest

• This sounds counter intuitive but over thousands of iterations, with each of them voting, achieves a number of things:
  • Identifies more difficult trends between the data.
  • Avoids overfitting as the model is more random and generalisable.
  • A more general but well analysed model, is more accurate.
  • Doesn’t heavily bias against a small group.

Thank you!

Questions?