Classification Part 1

Fundamentals of Machine Learning for NHS using R

Classification

 

• Part 1 Logistic Regression
• Part 2 Decision Trees & Random Forests

Logistic Regression

Logistic Regression

 

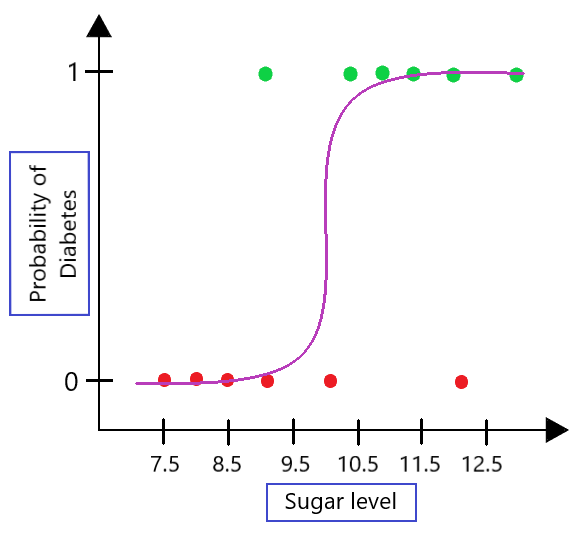
• Logistic regression is foremost used to model a binary (0,1) variable \(Y\), based on one or more other variables, called predictors.
• The binary variable being modelled is generally referred to as the response variable, or the dependent variable.

Logistic Regression

 

• For a model to fit the data well, it is assumed that:
  • The predictors are uncorrelated with one another.
  • That they are significantly related to the response variable.
  • The observations or data elements of a model are also uncorrelated.

Logistic Regression

 

• Logistic regression is typically utilised for 3 purposes:
  • To predict the probability that the response variable \(Y\) is equal to 1.
  • To categorise outcomes or predictors.
  • To assess the odds or risk associated with model predictors.

Logistic Regression

 

Aim: To predict the dependent variable \(Y\). \[P(Y=0)=1-P(Y=1)\] Denote \(k\) independent variables \[x_1,x_2, .,x_k\]

Logistic Regression

 

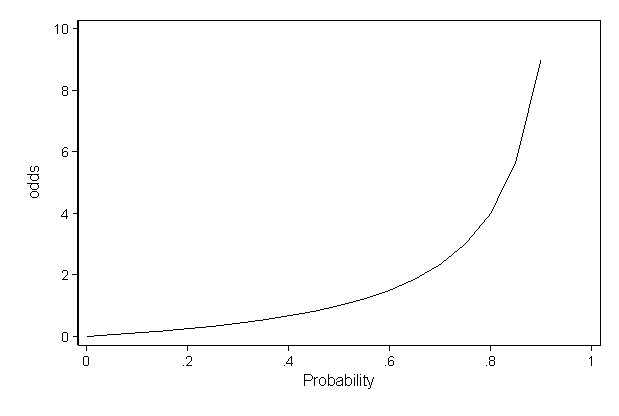
• At the centre of logistic regression analysis is the task of estimating the log odds of an event. \[ Odds = P(Y=1)/P(Y=0) \]
• Odds \(> 1 if (Y=1)\) is more likely
• Odds \(< 1 if (Y=0)\) is more likely

Logistic Regression

Suppose we roll a dice numbered 1 to 6 and we are interested in the outcome of rolling greater than a 2. \[ P(Roll>2) = 4/6 \\ P(Roll \leq 2) = 2/6 \] Therefore, the odds of rolling >2 \[ Odds=P(Roll>2)/P(Roll \leq 2)= 4/2 = 2 \] Odds 2:1

Logistic regression

However, there is a problem using this calculation in the model. If probability =1 then \[ Odds = 1/0= \infty \]
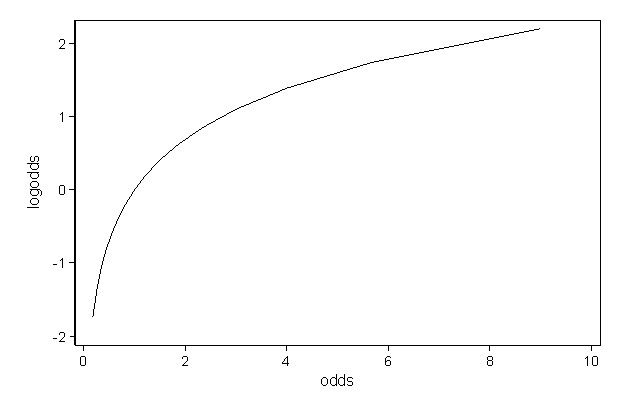
So, we use log odds instead. \[ Odds = Ln(P(Y=1)/P(Y=0) ) \] It maps probability ranging between 0 and 1 to log odds ranging from negative infinity to positive infinity.

Logistic regression

Logistic Regression

 

From mathematics, it can be shown that: \[ Ln\frac{P(Y=1)}{P(Y=0)}=\beta_0+\beta_1x_1+\beta_2x_2+\ldots+\beta_k x_k \] Hence we need to rearrange this function in terms of P(Y=1).

Logistic Regression

 

Given the fact that \[ \frac{P(Y=1)}{P(Y=0)}=\frac{P(Y=1)}{1 - P(Y=1)} \]

Logistic Regression

 

Taking logs of both sides you get \[ \frac{P(Y=1)}{1 - P(Y=1)} = e^{\beta_0+\beta_1x_1+\beta_2x_2+\ldots+\beta_k x_k} \]

Logistic Regression

 

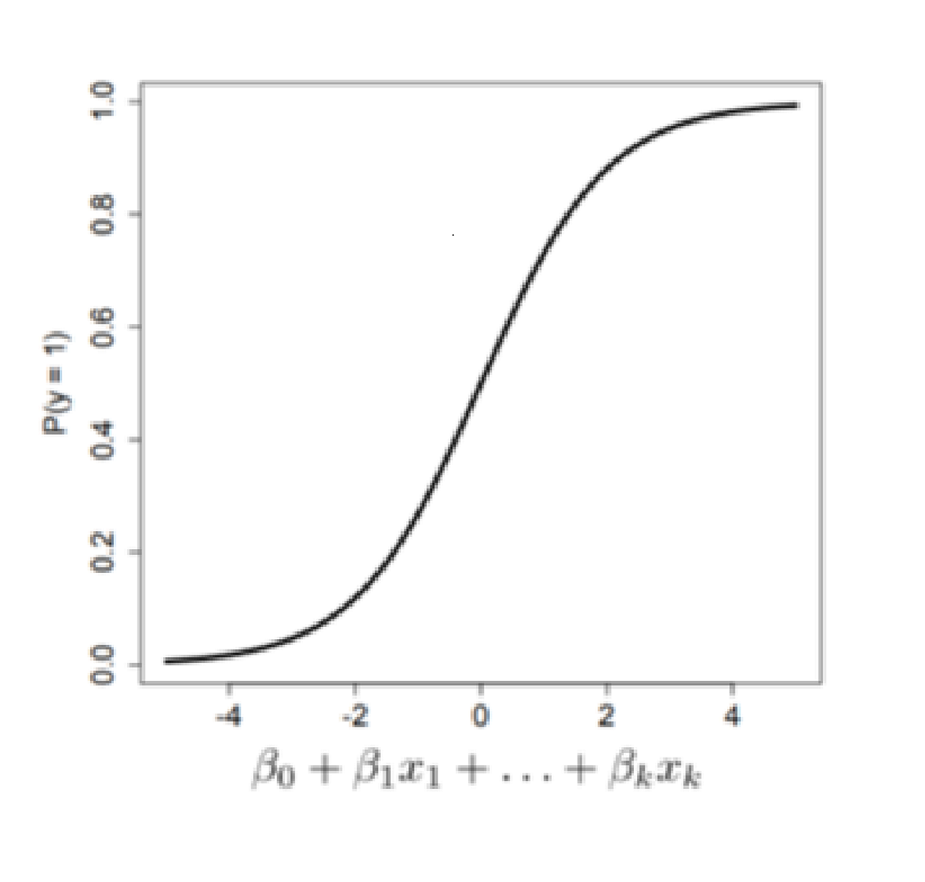
The logit function or the log-odds is therefore \[ P(Y=1) = \frac{1}{1 + e^-(\beta_0+\beta_1x_1+\beta_2x_2+\ldots+\beta_k x_k)} \]

Logistic Regression

 

• Positive values are predicted as class 1
• Negative values are predicted as class 0
• The coefficients are selected to:
  • Predict a high probability for the positive cases
  • Predict a low probability for the low cases

Logisitc Regression

Logistic Regression

 

• After fitting the model, it is likely that researchers will want to examine the contribution of individual predictors.
• To do so, they will want to examine the regression coefficients.
• In logistic regression, there are several different tests designed to assess the significance of an individual predictor.

Logistic Regression

 

• The AIC provides a method for assessing the quality of your model through comparison of related models.
• Unlike adjusted R-squared, the number itself is not meaningful.
• If you have more than one similar candidate models, then you should select the model that has the smallest AIC.
• So its useful for comparing models, but isn’t interpretable on its own.

Workshop: Logistic Regression

The source for this example is the Pima Indian Diabetes 2 data set obtained from the UCI Repository of machine learning databases (Newman et al. 1998).

Thank you!

Questions?